Where regular expressions fail to provide the necessary force we use Parsers. Discover how to build military grade parsers that can be used for any filtering or matching needs.

Table of contents

1. Marsec
2. Introduction

Marsec

We will be building a tool that allows us to convert Markdown files to HTML files

# Title
normal paragraph

to

<title>Title</title>
<p> normal paragraph <p>

What is a Parser

A parser is a piece of code that can takes in input a stream of tokens(read this blog for in-depth look into tokenization the input and builds a data structure that represents some logic, don't worry if this doesn't make sense. The thing about Parsers is that unlike regex or some finite sequence machine that you hot wired together to match against expressions they can match against expressions that nest arbitrarily deep like this expression (2+(3+4)) where we have an expression 3+4 whose result is inside another expression. regex and other forms of regular grammars are only good for linear matching.

user@> parser(1 + 1) 

    +
  /   \
 1     1 

See how we have added meaning to string above. + is a function that has 2 arguments which in this case are 1. Still doesn't make sense ? lets look at how English works.

Unwrapping English

To talk to each other we have to follow some rules and those rules for English are called English Grammar rules.
Information fundamentally is structured

"Something this very sense makes" doesn't make sense right, why ? It's because it doesn't follow grammar rules and so we cant understand the intention of the sentence.

Lets try this exercise, I will write ba set of grammar rules and we have to check if it passes against a list of sentences.

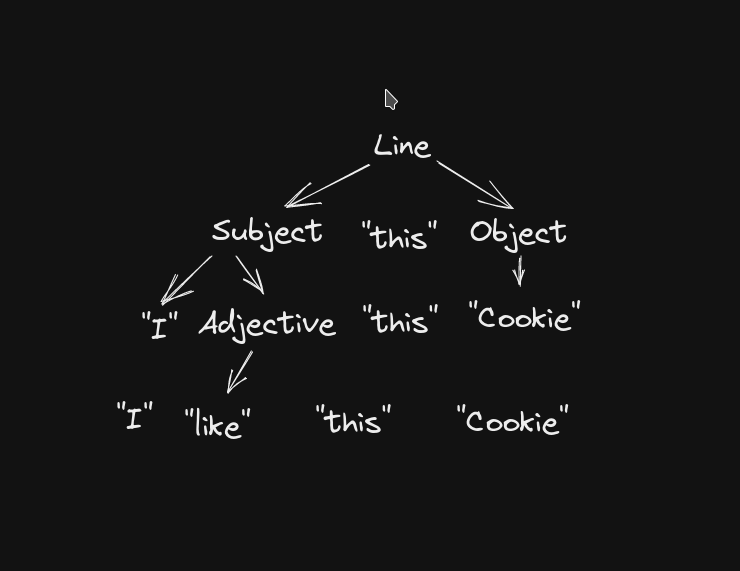
- Line      -> *Subject* "this" *Object*  
- Subject   -> "I" *Adjective*   
- Adjective -> "like" | "dislike"  
- Object    -> "Cookie" | "Car" | "pen"  

Note: The pipe | here just means or i.e. Object can be Cookie or Car or pen

Now given a line "I like this Cookie" we can check against the given grammar rules by using simple substitution on place holders like Subject, Adjective. In the field of Parsers we call these place holders non-terminal and we call like, Cookie, Car (words which cannot be substituted anymore) terminals.

Let's break down the above grammar and see if it fits the given sentence.

- Line      -> *Subject* "this" *Object*
- Subject   -> "I" *Adjective*
- Adjective -> "like"
- Object    -> "Cookie"  

Line => "I" "like" "this" "Cookie" => "I like this Cookie"

the above sentence is valid ✅ in our language as it can correctly consumes the whole string with the given grammar. With that every non-terminal has expanded until it only contains terminals and we have:

BNF (Backus-Naur Form) notation

Let's formalise the Grammar rules that we have been working with, from now we will be using BNF notation to describe the formal syntax of languages. In BNF we have a set of rules called productions like :

<non-terminal> ::= <expression>

• non-terminal as the name suggests is not terminal(end), it can expand to other expressions which are laid in the subsequent production rules.
• here the symbol ::= represents a relation between the non terminal and the expression it can expand to.
• terminals or constants are values that don't change like 1,2,3 or or.

Examples

Let's build on what we have learned by looking at some examples

• A primitive grammar that allows only numbers, no operations no functional definitions but just numbers:

<number> ::= 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0

• A grammar that allows addition looks like:

<expression> ::= <binary> | <number>
<binary>     ::= <expression> + <expression>  
<number>     ::= 1 | 2 ... 9 | 0

An expression can be represented as a binary or a number where number expands to a digit from 0 to 9 and binary is an expression plus another expression. Something like 1+2 is perfectly recognised by our language as:

1 + 2 ::= <binary> (rule 1)
1            +          2
|                       |
<expression> +  <expression> (rule 2)
|                       |
<number>     +       <number> (rule 1)
|
1            +        2  (rule 3)

What about this expression 1 + 2 + 3 ?
We see that this grammar is ambiguous as it can generate 2 representations for this expression.

          <expression>
              |
          <binary>
          /      \
 <expression>  <expression>
      |             |
    <binary>        <number>
   /       \
<expression> <expression>
     |             |
 <number>        <number>
     |             |
     (             3
    / \
<number> <number>
  |       |
  1       2                                     

          <expression>
              |
          <binary>
          /      \
 <expression>  <expression>
      |             |
  <number>         <number>
      |             |
      1             2
                     |
                     3

This is because in the first case we considered addition to be left associative i.e. 1+2+3 == (1+2)+3 and right associative in the next one. To remove this ambiguity we change our grammar and add rules for associativity which looks like:

<expression> ::= <binary> | <number>
<binary>     ::= <number> + <expression>  
<number>     ::= 1 | 2 ... 9 | 0

This grammar is right associative and produces a single representation for arbitrarily deep expressions like 1+2+3 which gives us just:

<expression>
   |
<binary>
 /      \
<number>  <expression>
   |          |
   1       <binary>
               /      \
          <number>  <expression>
             |         |
             2       <number>
                         |
                         3

similarly this is left associative

<expression> ::= <binary> | <number>
<binary>     ::= <expression> + <number>  
<number>     ::= 1 | 2 ... 9 | 0

Glossary

• Sentence: A combination of Words, doesn't have to make sense.
• Production: Rules by which the grammar works
• Terminal: In a sense they are the endpoints for the grammar rules like "Cookie" in the above example for the Object production.
• Non-Terminal: A non-terminal is a named reference to another rule in the grammar. It means “play that rule and insert whatever it produces here”. In this way, the grammar composes.

Helpful Links:

• BNF